Acid-base equilibria are an essential part of chemistry, and the determination of the acid dissociation constant (Ka) is critical for understanding these systems. PH is a measure of the acidity or basicity of a solution. It can be used to calculate the Ka value for a weak acid or base. In this article, we will explore how to find Ka from pH and the importance of understanding acid-base equilibria.
Understanding Acid-Base Equilibria
Acid-base equilibria refer to the chemical reactions between acids and bases that occur in a solution. In a chemical reaction, the reactants will form products, and the equilibrium is reached when the rate of the forward reaction equals the rate of the reverse reaction. The chemical equation for an acid-base reaction involves the transfer of a proton (H+) from the acid to the base.
Acids are defined as substances that donate protons, while bases are substances that accept protons. The strength of an acid or base is determined by its ability to donate or accept protons. Strong acids completely dissociate in water, while weak acids only partially dissociate.
When a weak acid is dissolved in water, it will undergo partial dissociation to form hydronium ions (H3O+) and the conjugate base. The acid dissociation constant (Ka) is a measure of the strength of the acid and is defined as the ratio of the concentration of the products to the concentration of the reactants.
Ka = [H3O+][A-] / [HA]
Where HA is the weak acid, A- is its conjugate base, and [H3O+] is the concentration of hydronium ions.
pH and Acid-Base Equilibria
pH is a measure of the acidity or basicity of a solution and is defined as the negative logarithm of the concentration of hydronium ions in the solution. The pH scale ranges from 0 to 14, where a pH of 7 is neutral, pH values below 7 are acidic, and pH values above 7 are basic.
In an acid-base equilibrium, the pH of the solution is related to the concentration of hydronium ions and the concentration of the weak acid or base. For example, the pH of a solution of acetic acid (CH3COOH) can be calculated using the acid dissociation constant (Ka) and the initial concentration of the acid.
CH3COOH + H2O ↔ H3O+ + CH3COO-
Ka = [H3O+][CH3COO-] / [CH3COOH]
pH = -log[H3O+]
By substituting [H3O+] in the pH equation with the expression derived from the Ka equation. We can obtain the following expression for pH in terms of the acid dissociation constant and the initial concentration of the acid.
pH = pKa + log([A-] / [HA])
Where pKa is the negative logarithm of the Ka value, and [A-] and [HA] are the concentrations of the conjugate base and weak acid, respectively.
How to Find Ka from pH
Finding Ka from pH involves solving for the acid dissociation constant (Ka) using the pH value and the initial concentration of the weak acid. The following steps can be used to find Ka from pH:
Determine the Initial Concentration of the Acid
The initial concentration of the weak acid can be determined from the volume of the solution and the molarity of the acid. For example, if we dissolve 0.1 moles of acetic acid in 1 liter of water, the initial concentration of the acid would be 0.1 M.
Calculate the H3O+ Concentration
The concentration of hydronium ions can be calculated from the pH value using the following equation:
[H3O+] = 10^(-pH)
For example, if the pH of the acetic acid solution is 4.5, the concentration of hydronium ions would be:
[H3O+] = 10^(-4.5) = 3.16 x 10^(-5) M
Calculate the Concentration of the Conjugate Base
The concentration of the conjugate base (CH3COO-) can be calculated using the initial concentration of the acid and the concentration of hydronium ions, as follows:
[CH3COO-] = Ka x [HA] / [H3O+]
Where Ka is the acid dissociation constant, [HA] is the concentration of the weak acid, and [H3O+] is the concentration of hydronium ions.
For example, if the initial concentration of acetic acid is 0.1 M and the concentration of hydronium ions is 3.16 x 10^(-5) M, and the Ka value for acetic acid is 1.8 x 10^(-5) at 25°C, the concentration of the conjugate base would be:
[CH3COO-] = (1.8 x 10^(-5)) x (0.1) / (3.16 x 10^(-5)) = 0.569 M
how to find Ka Value
The Ka value can be calculated using the concentrations of the weak acid, the conjugate base, and the hydronium ions, as follows:
Ka = [H3O+][A-] / [HA]
Where [H3O+], [A-], and [HA] are the concentrations of hydronium ions, conjugate base, and a weak acid, respectively.
For example, using the values obtained above, the Ka value for acetic acid would be:
Ka = (3.16 x 10^(-5)) x (0.569) / (0.1) = 1.8 x 10^(-5)
Importance of Understanding Acid-Base Equilibria
Understanding acid-base equilibria are essential in many fields, including medicine, environmental science, and industry. For example, in medicine, the acid-base balance of the body is critical for proper physiological function. Imbalances in acid-base equilibrium can lead to health problems such as acidosis or alkalosis.
In environmental science, acid-base equilibria play a vital role in understanding the chemistry of water systems. For example, acid rain is a result of acid-base equilibria in the atmosphere, where sulfur dioxide and nitrogen oxides react with water to form sulfuric acid and nitric acid, respectively.
In industry, understanding acid-base equilibria are essential for many chemical processes, including the production of pharmaceuticals, fertilizers, and plastics. The control of pH in these processes is critical for optimizing reaction rates, product yield, and purity.
how to find ka from PKA
The dissociation constant of an acid (Ka) and its negative logarithm (pKa) are related by the following equation:
pKa = -log(Ka)
To find Ka from pKa, you can use the following equation:
Ka = 10^(-pKa)
Here, the exponent (-pKa) is the negative of the pKa value, so you can simply take 10 to the power of the negative pKa to get the Ka value.
For example, if the pKa of an acid is 4.75, you can find its Ka as follows:
Ka = 10^(-4.75)
Ka = 1.78 x 10^(-5)
So, the Ka of the acid is 1.78 x 10^(-5).
If you know the pH of the solution containing the acid, you can use the Ka value to calculate the concentration of the acid. The equation for the acid dissociation constant can be written as:
Ka = [H+][A-]/[HA]
where [H+] is the hydrogen ion concentration, [A-] is the concentration of the conjugate base of the acid, and [HA] is the concentration of the undissociated acid.
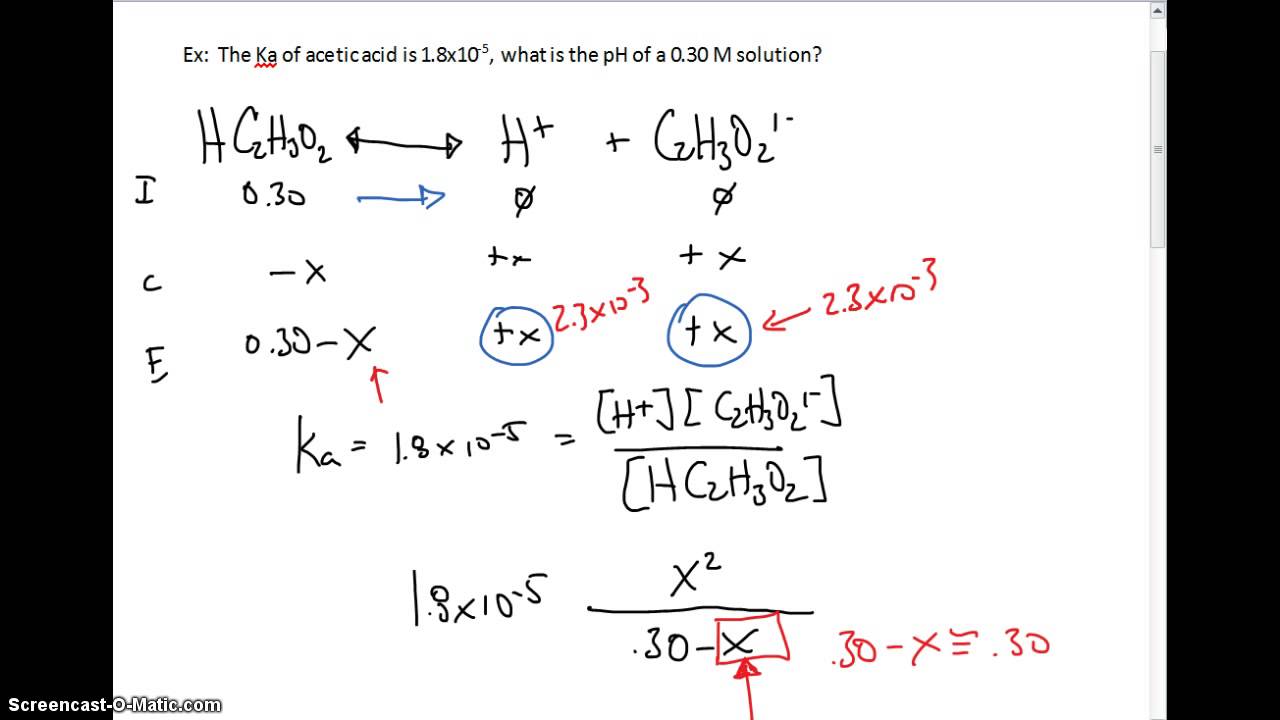
If the acid is weak, then the dissociation reaction can be assumed to be in equilibrium, and you can use the equilibrium constant expression to solve for the unknown concentration. For example, let’s say you have a solution of acetic acid (CH3COOH) with a pH of 4.8. The pKa of acetic acid is 4.76. You can use the Ka value to calculate the concentration of the acid:
Ka = 10^(-pKa) = 1.8 x 10^(-5)
At equilibrium,
At equilibrium, the concentration of the acid that has dissociated is equal to the concentration of the conjugate base (CH3COO-) that has been formed, so:
[CH3COOH] = [CH3COO-]
Let x be the concentration of the acid that has dissociated. Then, the concentration of the conjugate base is also x. The initial concentration of the undissociated acid is equal to the total concentration of the acid:
[HA] = [CH3COOH] + x
The hydrogen ion concentration can be calculated from the pH:
pH = -log[H+]
[H+] = 10^(-pH) = 10^(-4.8)
Now, we can substitute these values into the equilibrium constant expression and solve for x:
Ka = [H+][A-]/[HA]
1.8 x 10^(-5) = (10^(-4.8))(x)/(0.1M + x)
Solving for x gives:
x = 1.3 x 10^(-3) M
Therefore, the concentration of acetic acid in the solution is:
[CH3COOH] = [HA] – x = 0.1 M – 1.3 x 10^(-3) M = 0.099 M
The concentration of the conjugate base is also 1.3 x 10^(-3) M, and the pH of the solution can be calculated using the equation:
Here pH = pKa + log([A-]/[HA])
pH = 4.76 + log(1.3 x 10^(-3)/0.1)
pH = 4.8
This confirms that the pH of the solution is indeed 4.8, as given in the problem statement.
how to find ka from ph
To find the acid dissociation constant (Ka) from a pH value. You will need to know the concentration of the acid and the pH of its solution. The dissociation of an acid can be represented by the following equation:
HA ⇌ H+ + A-
where HA is the acid and A- is the conjugate base.
The Ka expression for this reaction is:
Ka = [H+][A-] / [HA]
where [H+] is the concentration of hydrogen ions, [A-] is the concentration of the conjugate base, and [HA] is the concentration of the acid.
To find Ka from pH, you first need to calculate the concentration of hydrogen ions using the pH formula:
pH = -log[H+]
Therefore, [H+] = 10^(-pH).
Next, you need to know the initial concentration of the acid (HA). If you do not know the initial concentration of the acid, you cannot calculate the Ka value.
Once you know the concentration of hydrogen ions ([H+]) and the initial concentration of the acid ([HA]), you can plug these values into the Ka expression and solve for Ka.
Ka = [H+][A-] / [HA]
Since the acid and its conjugate base are in equilibrium, the concentration of the conjugate base is equal to the concentration of hydrogen ions, so [A-] = [H+].
Therefore, Ka = [H+]^2 / [HA]
Substitute [H+] = 10^(-pH) and the initial concentration of the acid ([HA]) into the equation above and solve for Ka.
Conclusion
In conclusion, the determination of the acid dissociation constant (Ka) from pH is an essential part of understanding acid-base equilibria. PH is a measure of the acidity or basicity of a solution and can be used to calculate the Ka value for a weak acid or base. The understanding of acid-base equilibria has significant implications in medicine, environmental science, and industry, making it an essential concept in chemistry.